Details

Given n feature vectors x ₁= (x ₁₁,…,x _1p ), ..., x _n = (x _n1,…,x _{n p} ) of dimension p and a positive integer k, the problem is to find k p-dimensional vectors m ₁,…,m _k that minimize the goal function, within-cluster sum of squares

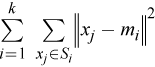
where S _i is a set of vectors to which m _i is the closest center. The vectors m ₁,…,m _k are called centroids. To start computations, the algorithm requires initial values of centroids.

Centroid Initialization

Centroid initialization can be done using these methods:

• Choice of first k feature vectors from the data set

• Random choice of k feature vectors from the data set using the following, simple random sampling draw-by-draw, algorithm:

  Let S contain all n feature vectors from the input data sets. The algorithm does the following:

  1. Chooses one of the feature vectors s _i from S with equal probability

  2. Excludes s _i from S and adds it to the sample

  3. Resumes from step 1 until the sample reaches the desired size k

Computation

Computation of the goal function includes computation of the Euclidean distance between vectors ||x _j - m _i ||. The algorithm uses the following modification of the Euclidean distance between feature vectors a and b: d(a,b) = d ₁(a,b) + d ₂(a,b), where d ₁ is computed for continuous features as

and d ₂ is computed for binary categorical features as

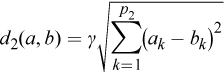
In these equations, γ weighs the impact of binary categorical features on the clustering, p ₁ is the number of continuous features, and p ₂ is the number of binary categorical features. Note that the algorithm does not support non-binary categorical features.

The K-Means clustering algorithm computes centroids using Lloyd's method [Lloyd82]. For each feature vector x ₁,…,x _n , you can also compute the index of the cluster that contains the feature vector.