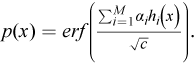Details

Given n feature vectors x ₁=(x ₁₁,…,x _1p),..., x _n=(x _n1,…,x _np) of size p, a vector of class labels y=(y ₁,…,y _n), where y _i ∈ K = {-1, 1} describes the class to which the feature vector x _i belongs, and a weak learner algorithm, the problem is to build a two-class BrownBoost classifier.

Training Stage

The model is trained using the Freund method [Freund01] as follows:

Calculate c = erfinv ²(1 - ε), where

erfinv(x) is an inverse error function,

ε is a target classification error of the algorithm defined as

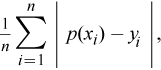
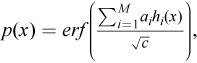
erf(x) is the error function,

h _i(x) is a hypothesis formulated by the i-th weak learner, i = 1,...,M,

α _i is the weight of the hypothesis.
Set initial prediction values: r ₁(x, y) = 0.
Set "remaining timing": s ₁ = c.
Do for i=1,2,... until s _i+1 ≤ 0
1. With each feature vector and its label of positive weight, associate
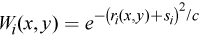
2. Call the weak learner with the distribution defined by normalizing W _i(x, y) to receive a hypothesis h _i(x)
3. Solve the differential equation
  
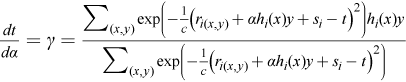
  with given boundary conditions t = 0 and α = 0 to find t _i = t* > 0 and α _i = α* such that either γ ≤ ν or t* = s _i , where ν is a given small constant needed to avoid degenerate cases
4. Update the prediction values: r _i+1(x, y) = r _i(x, y)+ α _i h _i(x)y
5. Update "remaining time": s _i+1 = s _i - t _i
End do

The result of the model training is the array of M weak learners h _i.

Prediction Stage

Given the BrownBoost classifier and r feature vectors x ₁,…,x _r, the problem is to calculate the final classification confidence, a number from the interval [-1, 1], using the rule