Details

Given a set X of n feature vectors x ₁= (x ₁₁,…,x _1p), ..., x _n= (x _n1,…,x _np) of dimension p, the problem is to find a maximum-likelihood estimate of the parameters of the underlying distribution when the data is incomplete or has missing values.

Expectation-Maximization (EM) Algorithm in the General Form

Let X be the observed data which has log-likelihood l(θ; X) depending on the parameters θ. Let X ^m be the latent or missing data, so that T=(X, X ^m) is the complete data with log-likelihood l ₀ (θ; X). The algorithm for solving the problem in its general form is the following EM algorithm ([Dempster77], [Hastie2009]):

Choose initial values of the parameters θ ⁽⁰⁾
Expectation step: in the j-th step, compute Q (θ', θ ^(j)) = E (l ₀ (θ'; T)|X, θ ^(j)) as a function of the dummy argument θ'
Maximization step: in the j-th step, calculate the new estimate θ ^(j+1) by maximizing Q(θ', θ ^(j)) over θ'
Repeat steps 2 and 3 until convergence

EM algorithm for the Gaussian Mixture Model

Gaussian Mixture Model (GMM) is a mixture of k p-dimensional multivariate Gaussian distributions represented as

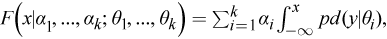
where Σ ^k _{i
= 1} α _i = 1 and α _i ≥ 0.

The pd( x|θ _i ) is the probability density function with parameters θ _i = (m _i , Σ _i ), where m _i is the vector of means, and Σ _i is the variance-covariance matrix. The probability density function for a p-dimensional multivariate Gaussian distribution is defined as follows:

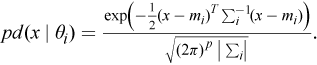
Let z _ij = I{x _i belongs to j mixture component} be the indicator function and θ=(α ₁, ..., α _k ; θ ₁, ..., θ _k).

Computation

The EM algorithm for GMM includes the following steps:

Define the weights as follows:

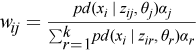
for i=1, ..., n and j=1, …, k.

Choose initial values of the parameters
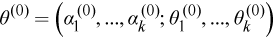
Expectation step: in the j-th step, compute the matrix W = (w _ij)_nxk with the weights w _ij
Maximization step: in the j-th step, for all r=1, ..., k compute:
1. The mixture weights
  
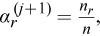
  where
  
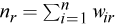
  is the "amount" of the feature vectors that are assigned to the r-th mixture component
2. Mean estimates
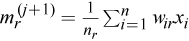
3. Covariance estimate
  
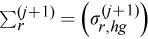
  of size p x p with
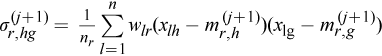
Repeat steps 2 and 3 until any of these conditions is met:
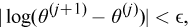
- where the likelihood function is
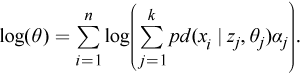
- The number of iterations exceeds the predefined level.

Initialization

The EM algorithm for GMM requires initialized vector of weights, vectors of means, and variance-covariance [Biernacki2003, Maitra2009].

The EM initialization algorithm for GMM includes the following steps:

Perform nTrials starts of the EM algorithm with nIterations iterations and start values:
- Initial means - k different random observations from the input data set
- Initial weights - the values of 1/k
- Initial covariance matrices - the covariance of the input data
Regard the result of the best EM algorithm in terms of the likelihood function values as the result of initialization