This section provides the syntax and semantics for the C/C++ language extensions for array notations.
Array Section Notation
In your application code, introduce a section operator in the standard C/C++ language, as follows:
section_operator ::= [<lower bound> : <length> : <stride>]
where the <lower bound>, <length>, and <stride> are of integer types, representing a set of integer values as follows:
<lower bound>, <lower bound + <stride>>, …, <lower bound> + (<length> - 1) * <stride>
A section operator can occur in place of a subscript operator. The following example is an array section with len elements: a[lb], a[lb + str], a[lb + 2*str], …, a[lb + (len-1)*str].
a[lb:len:str]
Length is chosen instead of upper bound because, in declarations, C/C++ deals with lengths of arrays and not upper bounds. Use of length also makes it easier to ensure that array sections match in size.
Successive section operators designate a sub-array of a multidimensional array object. When absent, the <stride> defaults to 1. If the <length> is less than 1, the array section is undefined. You can also use [:] as a short hand for a whole array dimension if the size of the dimension is known from the array declaration. If either <lower bound> or <length> must be specified, you must specify both.
| Example |
|---|
a[0:3][0:4] // refers to 12 elements in the 2D array a, starting at
// row 0, column 0, and ending at row 2, column 3.
b[0:2:3] // refers to elements 0 and 3 of the 1D array b
b[:] //refers to the entire array b
|
Array Declarations for Array Notations
For the array section notation—[:]—to be useful, the compiler must know the shape and size of an array object. The table below summarizes the different ways of declaring arrays and pointers to array objects in C/C++.
| Length | Storage Class | Declaration |
|---|---|---|
| Fixed | Static |
static int a[16][128] |
| Auto |
void foo(void) {
int a[16][128];
}
|
|
| Parameter |
void bar(int a[16][128]); |
|
| Heap |
int (*p2d)[128]; |
|
| Variable (C99) | Auto |
void foo(int m, int n) {
int a[m][n];
}
|
| Parameter |
void bar(int m, int n, int a[m][n]); |
|
| Heap |
void bar(int m, int n){
int (*p2d)[n];
}
|
The variable length array (VLA) notation is a C99 [ISO/IEC 9899] feature and a compiler specific-extension of C++. It is supported by the GNU GCC and Intel® C++ compilers.
Note
You must use the /[Q]std=c99 compiler option for the compiler to accept the C99 extensions.
If the base of an array section has incompletely specified dimensions (such as a pointer variable), you must explicitly specify the length of the array section. This is illustrated in the following example.
| Example |
|---|
typedef int (*p2d)[128]; p2d p = (p2d) malloc(sizeof(int)*rows*128); p[:][:] // error p[0:rows][:] // ok |
Operator Maps
Most C/C++ operators are available for array sections: +, -, *, /, %, <, ==, >, <=, !=, >=, ++, --, |, &, ^, &&, ||, !, -(unary), +(unary), +=, -=, *=, /=, *(pointer de-referencing). Operators are implicitly mapped to all elements of the array section operands. The operations on different elements can be executed in parallel without any ordering constraints.
Array operands in an operation must have the same rank and size. Rank is defined as the number of array section operators, and size is the length of each array section. A scalar operand is automatically filled to the whole array section of any rank.
| Example |
|---|
a[:] * b[:] // element-wise multiplication
a[3:2][3:2] + b[5:2][5:2] // addition of the 2x2 matrices in a and b
// starting at a[3][3] and b[5][5]
a[0:4] + b[1:2][0:4] // error, different rank sizes
a[0:4][1:2] + b[0][1] // adds a scalar b[0][1] to an array section.
|
Assignment Maps
The assignment operator applies in parallel to every element of the array section on the left hand side (LHS).
| Example |
|---|
a[:][:] = b[:][2][:] + c; e[:] = d; e[:] = b[:][1][:]; // error, different rank a[:][:] = e[:]; // error, different rank |
If there is an overlap between the RHS and the LHS, the behavior is undefined. There is no guarantee that the RHS will be evaluated before assignment to the LHS. If there is aliasing between the LHS and the RHS, the programmer must introduce a temporary array section to evaluate the RHS before assigning to the LHS. One exception is when there is an exact overlap and the stride is the same, then the assignment is well defined. This semantic allows for the most efficient code to be generated.
| Example |
|---|
a[1:s] = a[0:s] + 1; // due to overlap the behavior is undefined temp[0:s] = a[0:s] +1; // introduce temporary section to resolve a[1:s] = temp[0:s]; // the aliasing a[:] += b[:]; // well-defined: there is exact overlap and stride 1 // a[:] = a[:] + b[:]; |
Gather and Scatter
When an array section occurs directly under a subscript expression, it designates a set of elements indexed by the values of the array section.
| Example |
|---|
unsigned index[10] = {0,1,2,3,4,5,6,7,8,9};
float out[10], in[10] = {9,8,7,6,5,4,3,2,1,0};
out[0:5] = in[index[0:5]]; // gather
out[index[5:5]] = in[0:5]; // scatter
for(int i = 0; i < 5; i++){
cerr << "out[" << i << "]" << out[i] << endl;
}
|
If the index values in a scatter array section overlap with each other, the values for the duplicated locations must be the same, otherwise, the final stored value after the scatter is undefined.
Depending on the target architecture option chosen, and if the scatter/gather support is available on the target architecture, the compiler may map the array notations operations to the appropriate hardware.
Array Implicit Index
In writing code that uses array sections, you may find it useful to explicitly reference the indices of the individual elements in a section. For example, you may decide to fill an array with a function of the element index, rather than with a single value. Conceptually, an array section operation can be thought of as expanding into a loop with an implicit index variable for each relative rank of the section. For each relative rank, the value of the implicit index variable ranges between zero and one less than the length of the triplet with that relative rank. The __sec_implicit_index operation returns the value of the implicit index variable for a specified relative rank. It behaves as a function with the following declaration:
intptr_t __sec_implicit_index(int relative_rank);
The argument must be an integer constant expression. For purposes of rank checking, the rank of an implicit index operation is zero, although it is reevaluated for each element, similar to an expression of rank one.
| Examples |
int A[10], B[10][10]; // To assign A[0] = 0, A[1] = 1, A[2] = 2,... use: A[:] = __sec_implicit_index(0); // Assign B[i][j] = i+j: B[:][:] = __sec_implicit_index(0) + __sec_implicit_index(1); // The value of __sec_implicit_index is independent of the starting value // of the section. In this example, the values are either 0 or 1, even though the // actual indices are x+i and y+j. // B[x][y] = 0^0, B[x][y+1] = 0^1, B[x+1][y] = 1^0, B[x+1][y+1] = 1^1 B[x:2][y:2] = __sec_implicit_index(0) ^ __sec_implicit_index(1); |
Reduction Operations
A reduction combines array section elements to generate a scalar result. Intel® Cilk™ Plus supports reductions on array sections. It defines a generic reduction function that applies a user-defined dyadic function and a generic mutating reduction function that applies the result of the reduction function. Intel® Cilk™ Plus also has nine built-in common reduction functions. The built-in functions are polymorphic functions that accept int, float, and other C basic data type arguments. The names and descriptions of reduction functions are summarized in the table below followed by details and examples.
| Function Prototypes | Descriptions |
|---|---|
| __sec_reduce(fun, identity, a[:]) |
Generic reduction function. Reduces fun across the array a[:] using identity as the initial value. Deprecated. |
| result __sec_reduce(initial, a[:], function-id) |
Generic reduction function that supports scalar types as well as C++ arithmetic classes. Performs a reduction operation across array, a[:], using the reduction function, function-id, with initial as the initial value. Returns the result of the reduction in result. |
| void __sec_reduce_mutating(reduction, a[:], function-id) |
Generic mutating reduction function that supports scalar types as well as C++ arithmetic classes. Performs reduction operation across array, a[:], using the mutating reduction function, function-id, with the result of the reducing operation, reduction, accumulated in the initial value. Returns nothing. |
| Built-in Reduction Functions | |
| __sec_reduce_add(a[:]) | Adds values passed as arrays. |
| __sec_reduce_mul(a[:]) | Multiplies values passed as arrays. |
| __sec_reduce_all_zero(a[:]) | Tests that array elements are all zero. |
| __sec_reduce_all_nonzero(a[:]) | Tests that array elements are all non-zero. |
| __sec_reduce_any_nonzero(a[:]) | Tests for any array element that is non-zero. |
| __sec_reduce_min(a[:]) | Determines the minimum value of array elements. |
| __sec_reduce_max(a[:]) | Determines the maximum value of array elements. |
| __sec_reduce_min_ind(a[:]) | Determines the index of minimum value of array elements. |
| __sec_reduce_max_ind(a[:]) | Determines the index of maximum value of array elements. |
| __sec_reduce_and (a[:]) | Performs bitwise AND operation of values passed as arrays. |
| __sec_reduce_or (a[:]) | Performs bitwise OR operation of values passed as arrays. |
| __sec_reduce_xor (a[:]) | Performs bitwise XOR operation of values passed as arrays. |
Generic reducing function: the function denoted by function-id can be a user-defined function, operator, functor, or lambda expression that require assignment on top of the operation, for example, operator+. The reduction function must be commutative. The element type of the array section is used for:
-
lookup and overload resolution of the reduction function
-
the assignment operator needed to assign the return value to the result
-
the copy constructor for the initial value to be assigned to the reduction variable used (if needed).
Note
The implementation allows for non-constant function pointers as the reduction function. Also, The returning reduction function can replace the original defined __sec_reduce(fun, identity, a[:]); reduction function with your user-defined function. The original defined reduction function is deprecated.
| Example |
|---|
... complex<double> a[N]; complex<double> result; ... result = __sec_reduce(complex<double>(0,0), a[:], operator+ ); ... |
Generic mutating reduction function: the function denoted by function-id can be a user-defined function, operator, functor, or lambda expression that requires assignment on top of the operation, for example, compound assignment operator+=. The reduction function must be commutative. The element type of the array section is used for lookup and overload resolution for the compound reduction function.
Note
An assignment operator is not needed for the mutating reduction case.
| Example |
|---|
... complex<double> a[N]; complex<double> result; ... result = complex<double>(0,0); __sec_reduce_mutating(result, a[:], operator+= ); ... |
Built-in reduction functions: the reduction operation can reduce on multiple ranks. The number of ranks reduced depends on the execution context. For a given execution context of rank m and a reduction array section argument with rank n, where n>m, the last n-m ranks of the array section argument are reduced.
| Example |
|---|
sum = __sec_reduce_add(a[:][:]); // sum across the whole array 'a' sum_of_row[:] = __sec_reduce_add(a[:][:]); // sum elements in each row of 'a' |
Shift Operations
A shift does a shift of the elements in the array section elements to generate a scalar result. Intel® Cilk™ Plus supports shift operations on array sections. The names and descriptions of shift functions are summarized in the table below. The shift and circular shift (rotate) functions are defined for rank one expressions.
| Function Prototypes | Descriptions |
|---|---|
| b[:] = __sec_shift(a[:], signed shift_val, fill_val) |
Generic shift function. Performs a shift operation on the elements of the array a[:] towards a higher/lower index value. A positive shift_val shifts towards lower index values while a negative shift_val shifts towards higher index values. The fill_val argument indicates the fill value of the array section element type that is used to fill the vacated elements. The result is assigned to the return value, b[:]. The array section argument, a[:] is not modified. |
| b[:] = __sec_rotate(a[:], signed shift_val) |
Generic rotate function. Performs a circular shift (rotate) of the elements in the array section, a[:]. A positive shift_val rotates towards lower index values while a negative shift_val rotates towards higher index values. The result is assigned to the return value, b[:]. The array section argument a[:] is not modified. |
Function Maps
Maps are implicitly defined on scalar functions. All the array section arguments in a scalar function map call must have the same rank. Scalar arguments are automatically filled to match any rank.
| Example |
|---|
a[:] = sin(b[:]); a[:] = pow(b[:], c); // b[:]**c a[:] = pow(c, b[:]); // c**b[:] a[:] = foo(b[:]); // user defined function a[:] = bar(b[:], c[:][:]); //error, different ranks |
Mapped function calls are executed in parallel for all the array elements, with no specific ordering. Vector functions may have side effects. When there are conflicts during parallel execution, the program semantics may be different from the serial program.
Function maps are powerful tools used to apply a set of operations in parallel to all elements of an array section.
Many routines in the svml library are more highly optimized for Intel® microprocessors than for non-Intel microprocessors.
Passing Array Section Arguments
Intel® Cilk™ Plus supports a vector kernel style of programming, where vector code is encapsulated within a function by declaring array parameters of fixed or parameterized vector lengths.
The address of the first element of an array section can be passed as argument to an array parameter. The following example illustrates how to combine array notation to achieve vectorization inside a function body using Intel® Cilk™ Plus threading for parallel function calls.
Note
The parameter float x[m] depending on an earlier parameter int m is only supported in C99 and not in C++.
| Example |
|---|
#include <cilk/cilk.h>
void saxpy_vec(int m, float a, float x[m], float y[m]){
y[:]+=a*x[:];
}
void main(void){
int a[2048], b[2048] ;
cilk_for (int i = 0; i < 2048; i +=256){
saxpy_vec(256, 2.0, &a[i], &b[i]);
}
}
|
By writing the function explicitly with array arguments, you can write portable vector codes using any threading runtime and scheduler.
Conditionals and if statements
Array sections can be used with the C/C++ conditional operator, or in the conditional test of an if statement.
| Example |
|---|
c[0:n] = (a[0:n] > b[0:n]) ? a[0:n] - b[0:n] : a[0:n];
// is equivalent to:
if (a[0:n] > b[0:n]) {
c[0:n] = a[0:n] – b[0:n];
}
else {
c[0:n] = a[0:n];
}
|
In the above example, each element c[i] of the result array c will be assigned either a[i]-b[i] or a[i], depending on whether a[i] > b[i].
When array sections are used in conditional expressions (either an if-statement condition or a conditional operator), all array sections in every statement in the "true" and "false" clauses must have the same shape.
Keep in mind that the hardware may need to compute both sides of the conditional and blend them together; the clauses should be kept short, if possible.
Limitations
There are two limitations on the usage of array sections:
-
Functions cannot return array section values. To receive output values, two techniques can be used:
Output array:
void addit(float out[N], float in[N]) { out[:] = in[:] + 4.5f; } float A[N],B[N]; addit(A,B);Function map:
float addit(float in) { return in + 4.5f; } float A[N],B[N]; A[:] = addit(B[:]);When the function is not inlined, there are differences in the number of function calls between those two approaches. The function map approach calls addit() N-times more than the output array approach, so plan accordingly.
-
The "true" and "false" clauses of conditional expressions with array sections must not contain the return, break, while, for, or goto statements. Nested if-statements are allowed.
Programming Hints and Examples
There is no cost associated with writing an application that mixes scalar and data parallel operations on the same arrays. The Intel compiler uses the array operations in the program to guide vectorization. The following example implements an FIR filter. The scalar code consists of a doubly nested loop where both the inner and outer loop can be vectorized. By writing the program in different ways using array notation, you can direct the compiler to vectorize differently.
| Example: FIR Scalar Code |
|---|
for (i=0; i<M-K; i++){
s = 0
for(j=0; j<K; j++){
s+= x[i+j] * c[j];
}
y[i] = s;
}
|
| Example: FIR Inner Loop Vector |
for (i=0; i<M-K; i++){
y[i] = __sec_reduce_add(x[i:K] * c[0:K]);
}
|
| Example: FIR Outer Loop Vector |
y[0:M-K] = 0;
for (j=0; j<K; j++){
y[0:M-K]+= x[j:M-K] * c[j];
}
|
The parallel array assignment semantics enable vectorization of computations on the right hand side (RHS) of the assignment even if the l-value of the assignment may alias with some operands on the RHS. Since the compiler does not automatically introduce temporary arrays when aliasing occurs one should add explicit temporary arrays to ensure the correct behavior, when in doubt. This may increase memory usage and incur extra overhead from writing and reading them, which needs to be amortized by the speed-up from vectorizing the code.
| Example: |
|---|
void saxpy_vec (int m, float a, float *x, float y[m]){
y[:] += a * x[0:m]; // Compiler assumes x and y are disjoint even if they are not
}
void saxpy_vec (int m, float a, float x[m], float y[m]){
float z[m];
z[:] = y[:]; // When in doubt, programmer has to introduce temporary array
// It is best to confirm whether there are any possibilities of overlap.
y[:] = z[:] + a * x[:];
}
|
To take full advantage of vector instruction set, it is often beneficial to use a fixed vector length supported by the processor, as illustrated in the next example. The example code computes an average over nine points in a two-dimensional grid (avoiding the 1-element boundary around the grid where the nine-point average is not defined). The core computation is written in vector form as in a function nine_point_average. The application is further parallelized using a cilk_for loop at the call site. The grain size of the computation is controlled by the two compile time constants, VLEN and NROWS, which designate the length of vector operations and the number of rows processed in each invocation. Because the loads of adjacent rows are reused across multiple rows, you gain on memory locality by processing multiple rows inside the function. Using compile time constant for vector length makes the vector code generation more efficient and predictable.
| Example |
|---|
#include <malloc.h>
#include <cilk/cilk.h>
#define VLEN 4
#define NROWS 4
//-------------------------------------------------------------------
// Vector kernel
// for each grid
// o[x][y] = (i[x-1][y-1] + i[x-1][y]+ i[x-1][y+1] +
// i[x][y-1] + i[x][y] + i[x][y+1] +
// i[x+1][y-1] + i[x+1][y] + i[x+1][y+1])/9;
// written with:
// 1) VLEN columns for vectorization
// 2) NROWS rows for the reuse of the adjacent row loads
//--------------------------------------------------------------------
void nine_point_average(int h, int w, int i, int j, float in[h][w], float out[h][w])
{
float m[NROWS][VLEN];
m[:][:] = in[i:NROWS][j:VLEN];
m[:][:] += in[i+1:NROWS][j:VLEN];
m[:][:] += in[i+2:NROWS][j:VLEN];
m[:][:] += in[i:NROWS][j+1:VLEN];
m[:][:] += in[i+1:NROWS][j+1:VLEN];
m[:][:] += in[i+2:NROWS][j+1:VLEN];
m[:][:] += in[i:NROWS][j+2:VLEN];
m[:][:] += in[i+1:NROWS][j+2:VLEN];
m[:][:] += in[i+2:NROWS][j+2:VLEN];
out[i:NROWS][j:VLEN] = 0.1111f * m[:][:];
}
//---------------------------------------------------------------------
// caller
//---------------------------------------------------------------------
const int width = 512;
const int height = 512;
typedef float (*p2d)[];
int main() {
p2d src = (p2d) malloc(width*height*sizeof(float));
p2d dst = (p2d) malloc(width*height*sizeof(float));
// …
// perform average over 9 points
cilk_for (int i = 0; i < height - NROWS - 3; i += NROWS) {
for (int j = 0; j < width - VLEN - 3; j += VLEN) {
nine_point_average(height, width, i, j, src, dst);
}
}
}
|
| Command-line entry |
icl /Qstd=c99 test.c //on Windows* icc -std=c99 test.c //on Linux* and OS X* with EDG compiler icl -std=c99 test.c //on OS X* with CLANG compiler |
Optimizing Data Layout for Array Notation Vectorization
Some applications may benefit from a data layout change that converts data structures written in an Array of Structures (AOS) representation to a Structure of Arrays (SOA) representation. This helps prevent gathers when accessing one field of the structure across the array elements, and helps the compiler vectorize loops that iterate over the array. Such data transformations should be done by you at the program level to avoid repeating costly transformations before and after each loop.
AOS to SOA conversion: The conversion of your data structures from an Array of Structures (AOS) to a Structure of Arrays (SOA) is a common optimization that helps prevent gathers and scatters in vectorized code. Maintaining separate arrays for each field of the structure keeps memory accesses contiguous and aids vectorization when operating over structure instances. The AOS representation requires gathers and scatters, which can impact both SIMD efficiency as well as introduce extra bandwidth and latency for memory accesses. The presence of a hardware gather-scatter mechanism does not eliminate the need for this transformation since gather-scatter accesses commonly need significantly higher bandwidth and latency than contiguous loads.
The SOA form does reduce the locality of multiple fields in a single instance of the original structure, which could increase Translation Look-aside Buffer (TLB) pressure. It may be preferable to use an Array of Structures of Arrays (AOSOA) data structure even if only traversing a subset of the structure’s instances. This provides the benefit of locality at the outer-level and unit-stride at the innermost-level. The length of the inner array can be a small multiple of vector length to take advantage of unit-stride full vectors. Each structure instance will have multiple fields laid out in small arrays. At the outer level, you will now have an array of larger structures. In such a layout, the field accesses will still be close enough to get the benefit of page locality for nearby structure-instance accesses in the original code.
Here is a simple example that shows the difference between these forms:
AOS Form (Array of Structures):
| Example |
|---|
struct node {
float x, y, z;
};
struct node NODES[1024];
float dist[1024];
for(i=0;i<1024;i+=16){
float x[16],y[16],z[16],d[16];
x[:] = NODES[i:16].x;
y[:] = NODES[i:16].y;
z[:] = NODES[i:16].z;
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i:16] = d[:];
}
|
SOA Form (Structure of Arrays):
| Example |
|---|
struct node1 {
float x[1024], y[1024], z[1024];
}
struct node1 NODES1;
float dist[1024];
for(i=0;i<1024;i+=16){
float x[16],y[16],z[16],d[16];
x[:] = NODES1.x[i:16];
y[:] = NODES1.y[i:16];
z[:] = NODES1.z[i:16];
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i:16] = d[:];
}
|
AOSOA Form (Array of Structures of Arrays OR Tiled Array of Structures):
| Example |
|---|
struct node2 {
float x[16], y[16], z[16];
}
struct nodes2 NODES2[64];
float dist[1024];
for(i=0;i<64;i++){
float x[16],y[16],z[16],d[16];
x[:] = NODES2[i].x[:];
y[:] = NODES2[i].y[:];
z[:] = NODES2[i].z[:];
d[:] = sqrtf(x[:]*x[:] + y[:]*y[:] + z[:]*z[:]);
dist[i*16:16] = d[:];
}
|
Multi-Dimensional Casting Operations
For arrays of two or more dimensions the C language uses row-major ordering. When porting code to array notation format, it is not uncommon to encounter array access patterns that are impossible to express using array notations. However, you can often convert the array into a form that is suitable.
For instance, consider that you want to access the data in the center of a 4x4 array.
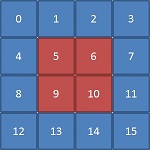
This 4x4 array can be represented as a two-dimensional array as follows:

If you are porting code in which this 2-dimensional data is represented as a 1-dimensional array there is no way to express this access pattern using array notation alone, unless you convert your array into a 2-dimensional one. You can do this as follows:
float (*array_2D)[4] = (float (*)[4])array_1D;
Using this method, the above access pattern can be made accessible as array notations as follows:
array_2D[1:2][1:2];
You can extend this approach to any dimensionality, as the following example illustrates.
| Example |
|---|
#define XRES 48 #define YRES 64 #define ZRES 48 float (*array_3D)[YRES][XRES] = (float (*)[YRES][XRES])array_1D; array_3D[1:ZRES-2][1:YRES-2][1:XRES-2]; |